Brock Engineering
P. O. Box 302, Roxbury CT 06783 (860)
354-7069
PROGRAMMING COMBINED DISCRETE-CONTINUOUS SIMULATION MODELS FOR PERFORMANCE
J. Frederick Klingener klingener@BrockEng.com
President, Brock Engineering, P.C.
Roxbury, Connecticut 06783, U.S.A
Presented at the 1996 Winter
Simulation Conference
Coronado, California, December 8-11, 1996
Proceedings of the 1996 Winter Simulation
Conference
ed. J. M. Charnes, D. M. Morrice, D. T. Brunner, and J. J. Swaine
Continuous state variables in combined discrete-continuous simulation models (combined models) commonly represent physical quantities, such as fluid levels or temperatures, that are governed by physical laws, and these laws are expressed as differential equations of state. The combined simulation modeling program commonly integrates the differential equations numerically, in step with its computations that describe the evolution of the discrete events. In addition to the pitfalls familiar to numerical integration, special hazards due to the interacting discrete events may confront the analyst seeking high performance in a complex model.
This paper first discusses, in the context of discrete event modeling packages, some requirements for obtaining accuracy and speed in the numerical integration of the continuous variables in combined models, and second, it describes approaches that can be used to meet those requirements in selected commercial modeling packages.
The distinguishing feature of combined
discrete-continuous simulation models (combined models) is the
existence of continuous state variables that interact in complex
or unpredictable ways with discrete events. The introduction of
continuous variables into a discrete event simulation sets two
tasks: 1) evaluation of the continuous variable itself often by
numerical integration of a governing differential equation, and
2) assuring proper interaction among the continuous and discrete
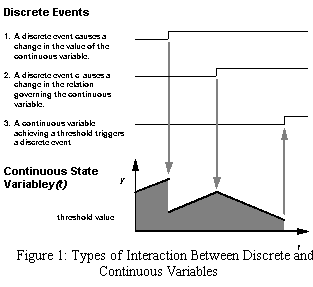
state variables. Figure 1 shows the three fundamental types of
interaction, described by Pritsker [1968], that can occur between
discrete and continuous variables: 1) a discrete event causes a
change in the value of a continuous variable, 2) a discrete event
causes a change in the relation governing the evolution of a
continuous variable, and 3) a continuous variable causes a
discrete event to occur or to be scheduled by achieving a
threshold value.

Combined modeling goes beyond the simple numerical integration of the continuous variables and specification of the particular interactions that may occur among continuous and discrete state variables; there is a fundamental mismatch between the way that time is advanced by a stack-based discrete event modeler and the way it is advanced by a marching continuous variable integrator. On the one hand, the common discrete event modeler is event-driven. It advances time asynchronously, that is it takes the execution time of an event from the top of a sorted stack, calculates its effect on the system state, schedules dependent events by placing them into appropriate places in the event stack, and advances the simulation clock to the next scheduled event. On the other hand, the common continuous variable solver is synchronous. It uses the system state at some time, t, to compute the value of a continuous state variable at some short time later at t + {delta} t. The solver then advances the simulation clock to t + {delta} t and continues.
Press et al. [1992] describe classical techniques used to perform the synchronous calculation with speed and accuracy. In the methods they describe, there is a tradeoff between accuracy and speed, and the determinant of the tradeoff is the time step size. If the integration proceeds using a large number of small time steps, then the accuracy can be high at the expense of computation speed. Conversely, in a solution that uses a small number of larger time steps to obtain rapid execution, the accuracy may suffer. The adaptive step size methods described by Press et al. [1992] have been developed to manage this classical tradeoff, but these methods depend on the freedom to adjust the time step size, t, in response to the local conditions relating to the integration process itself. If the time step size is subject to outside constraints, such as might be required to detect and respond with sufficient resolution to discrete events, then performance may suffer.
The purpose of this paper is to describe techniques that an analyst can use to build high performance combined models by reconciling the mismatch between the views of time held by the discrete event modeler and the numerical integrator while preserving the theoretical bases and implementation methods of the classical methods of high performance numerical integration of continuous variables. The second section of this paper discusses first an overall strategy that enables the techniques, and second the details of managing the three types of interaction between discrete events and continuous state variables. (TOC)
2.0 IMPLEMENTING NUMERICAL METHODS IN A COMBINED MODEL
The first step in adapting the numerical integrator to the discrete event environment is to recognize that the continuous state variable may be only piecewise smooth between the interacting events. A numerical procedure that seeks high accuracy should reflect this structure. The second step is to acknowledge that, given the system state when the simulation clock stands at time t, any value computed for a continuous variable y some time t in the future is speculative. It must be considered invalid until the simulation clock reaches t + {delta} t without encountering any event or condition that affects the continuous variable or the relation that governs its evolution. The subsections that follow first describe an approach to the implementation of speculative computation. Then they outline strategies for programming the three types of interactions between discrete events and the piecewise smooth state variables. (TOC)
As a minimum procedure, when the value of y( t + {delta} t) is computed at time t, it must be considered speculative and saved locally or privately, then published for use by
other processes only when it becomes valid. Apart from assuring consistency in the integration of the continuous variables, this strategy enables the techniques for managing the interactions between continuous and discrete variables described in the next three subsections.
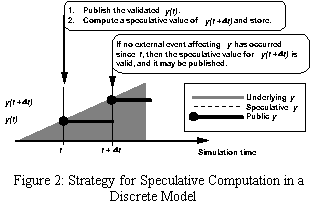
Figure 2 shows a schematic of the method. In this figure and in the three figures that follow, a continuous state variable, y, is evaluated numerically as a function of time at increments of t, given an expression for its rate of change. The underlying value of y(t) is shown as a gray line, the speculative (local) value of y(t) is a dashed line, and the validated (public) value of y(t) is a solid black line. When the simulation clock arrives at time t without encountering some invalidating event, the speculative value of y(t) may be published or made available to other processes. Then, the system state at t may be used to project a speculative value of y at t + {delta} t. This speculative y, invalid until t + {delta} t, is stored privately or locally, and the clock may be advanced.
Figure 2 also illustrates a secondary point about combined models. Note that the solution for y(t) can approach arbitrarily high accuracy (matching the underlying y) at t and again at t + {delta} t, but there will be an error at other times. For this reason, it is desirable to synchronize the numerical integration of related continuous variables. Under circumstances where this is not practical, it may be necessary to store enough of the state at time t to permit another process to reconstruct y at an intermediate time.
The speculative computation facilitates programming of the interactions between continuous variables and discrete events. In general, if an interacting discrete event happens between t and t + {delta} t, then the speculative value of y(t + {delta} t) must be abandoned, a current value of y, must be calculated and published, and a new speculative value of y must be calculated and stored. The following subsections describe how interacting discrete events that happen between t and t + {delta} t affect the subsequent calculations of y(t) for the three types of interactions described in section 1. (TOC)
2.2 Interaction Type 1: A Discrete Event Changes the Value of a Continuous Variable
Figure 3 shows a procedure for programming the
numerical integration of a continuous variable in the vicinity of
a Type 1 interaction, in which a discrete event causes a change
in the value of a continuous variable. The objectives of the
procedure are to manage the transition between piecewise smooth
segments by the following steps: 1) terminate the segment that
ends with the interrupt, 2) reset the continuous state variable
to the new value, and 3) restart the integration with a new
segment. Figure 3 shows that at t (the time step
immediately before an interrupting event), the procedure is the
same as that shown in figure 2 - the validated y(t) is
published and a speculative y(t + {delta} t) is computed
and stored. At t1, in response to a
discrete event that sets the value of y to y1,the
following steps are programmed: 1) the speculative value of y(t
+ {delta} t) is abandoned, 2) y1 is
published as the valid y, and 3) a revised speculative y(t1
+ {delta} t) is calculated and stored.
2.3 Interaction Type 2: A Discrete Event Affects the Relation Governing a Continuous Variable
Interactions of the second type (a discrete
event causing a change in the relation governing the evolution of
a continuous variable) can be programmed in a similar way, as
Figure 4 shows. The principal difference between this case and
the Type 1 interaction is that in the Type 1 case, the value of y(t1)
is specified by the interrupting process, while in this Type 2
case, the value of y(t1) must be
calculated by the integrating process itself before publishing.
The performance requirements of the particular model dictate the
level of sophistication required in this calculation of y(t1)
in the Type 2 case. In the simplest case, perhaps the
value of y(t1) could be simply
interpolated between y(t) and y(t + {delta} t),
while a more demanding case might require prior storage of all of
the required elements of the system state at t to enable a
complete reconstruction of y(t1).
2.4 Interaction Type 3: A Continuous Variable Achieving a Threshold Causes a Discrete Event
The processing of a Type 3 interaction (an interaction in which the continuous variable achieving a threshold causes a discrete event to occur) differs in two fundamental ways from the processing of Type 1 and Type 2 interactions: 1) the integration process itself identifies the time of the interaction, and 2) the integration process triggers discrete events. Figure 5 shows the strategy for programming a Type 3 interaction. At t, the speculative value y(t + {delta} t) may be checked to see whether y has crossed the threshold. If no crossing is found, then the process may continue in the simple form shown in figure 2. If a crossing has occurred, then the integrating process must find the time of crossing by a method that gives suitable accuracy. Again, the performance requirements of the particular application guide the choice of a method. In the simplest case, the crossing time tthreshold may be estimated by interpolating the value of y(t) between t and t + {delta} t, while for more demanding applications, a root-finding procedure might be required.
Type 3 interactions additionally require that the modeling program provide special features not required for the other types of interactions. The numerical integrating process must be able 1) to trigger discrete events immediately (at tthreshold in the example), 2) to
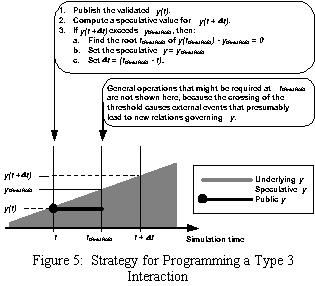
cause discrete events to be scheduled, and 3) to reset or adjust other continuous variables and relations that govern them. (TOC)
3.0 SUMMARY
Continuous state variables in combined models are composed of piecewise smooth functions of time, divided by discrete events into continuous segments. If synchronous integration methods are used, then the precision with which boundary events can be resolved depends on the selection of integrating time step - the smaller the step, the finer the resolution. To meet resolution requirements, the analyst may place an upper bound on the permissible time step size in addition to that dictated by the needs for accuracy in the integration process itself. This additional constraint may result in a performance penalty. Using asynchronous (event-driven) integration methods to divide the smooth pieces removes the need for the additional constraint
Figure 6 summarizes the differences between synchronous and asynchronous integration. In the case of synchronous integration, the fidelity with which the computed result reflects the interactions with discrete events clearly depends on the selection of step size. In the case of asynchronous integration, the continuous state variable is divided into its three piecewise smooth segments. In the case of the Types 1 and 2 interactions, the division reflects the "exact" time resolution of the discrete event scheduler, and in the case of the Type 3 interaction, the time resolution of the detection threshold can be made arbitrarily fine. Thus, fidelity at the segment boundaries is independent of the integration step size.
The earlier sections of this paper discussed the methods of speculative computation and asynchronous integration that are needed to adapt classical numerical integration methods, which are basically synchronous, to the asynchronous environment of the commercial discrete modeler. This section first discusses general programming features (data structures and function calling conventions) that are useful for implementing those methods. Then, for two commercial modelers, it discusses how the analyst can exploit programming features and how a simple example model can be programmed. An exploration of comparative performance or even preference is outside the scope of this paper. (TOC)
The notions critical to adaptation of classical numerical integration methods to a discrete event environment are: 1) speculative computation described in section 2.1and 2) interruptible processes to enable the methods described in sections 2.2 through 2.4. To implement speculative computation, it is useful, though not necessary, for the modeler's data structure to embody some idea of locality or privacy to protect the speculative values of the continuous state variables until they can be validated. Further, the modeler should have some facility for interrupting the integration process so that the speculative values of continuous state variables can be modified to reflect changes due to discrete events that occur between computation and validation. This section discusses approaches to combined modeling that can be used with two modelers ProModel for Windows (ProModel Corporation, Orem UT) and Extend (Imagine That!, San Jose CA).
As a framework for discussion, the following simple system was constructed in both models: pallets containing massive steel objects arrive at a preparation area. When space is available, a pallet is loaded into a furnace, in which it is heated by radiation and convection, to a predetermined threshold temperature. Then the pallet is moved to a cooling area and then to disposal. The pallet temperature is a represented by a continuous state variable that follows the differential equations of heat flow. The variable is divided into smooth pieces by the charging and discharging events.
The model includes interactions of all three types, the arrival of a pallet in the furnace combines types 1 and 2 interactions by setting both the value of the continuous state variable and the relation governing it. The type three interaction occurs when the pallet temperature reaches the threshold temperature. (TOC)
ProModel for Windows (PMW) is a discrete event modeler that has no explicit support for modeling continuous processes. It does have features that an analyst can use to build integrators that implement the techniques that section 2 describes. PMW has a useful data structure that includes real and integer variables with either global or local scope. In addition, the user can define real or integer attributes for entities and/or locations. PWM provides at least two constructs that can be used to program numerical integrators: 1) subroutines launched by the ACTIVATE statement, and 2) operations code that is executed by arrival of an entity at a location. This section takes the latter approach.
Klingener [1995] describes a combined model built in PMW based on a synchronous Euler integration scheme using the approach. Although the methods were useful for illustrating the technique of embedding numerical integration schemes in entity operations code, they are not suitable for serious modeling. Adding such features as speculative computation, a robust integration scheme, adaptive time stepping, and Type 3 interactions no change to the basic structure of the model. However, managing interactions of Types 1 and 2 requires the creation, by interrupting events (using PMW's ORDER statement), of dummy entities that update the continuous variable as required, that arrange the orderly termination of the already running Operations code, and that flush invalid speculative results.
The programming is described here from the bottom up. Listing 1 shows the subroutine deriv1 that returns the rate of change of the charge temperature, given the simulation clock time and the state variables. Listing 2 shows the dy_rk4 subroutine that implements the 4th order Runge-Kutta numerical integration method. It calls the deriv1 routine and returns the change in temperature during the integration time step.
Listing 1: Differential Change in Temperature
# real deriv1(real time,
real charge_temp)
#--------------------------------------------------------------
# uses global variables:
# area - heat transfer area (ft^2)
# charge_weight (lbf)
# specific_heat (BTU/lbf/degR)
# Hconv - convect. h. t. coeff (BTU/hr/ft^2/degR)
# Hrad - rad. h. t. coeff (BTU/hr/ft^2/degR^4)
RETURN
(area/(charge_weight*specific_heat))*
(Hconv*(Thigh-charge_temp) +
Hrad*(Thigh**4-charge_temp**4))
Listing 2: Fourth Order Runge-Kutta Procedure
# real dy_rk4(real x, real
y, real dx)
#--------------------------------------------------------------
# unadorned fourth order Runge_Kutta
# ref Press, et al. 2nd Ed. page 711 eqn 16.1.3
REAL k1,k2,k3,k4
k1=deriv1(x ,y )*dx
k2=deriv1(x+dx/2,y+k1/2)*dx
k3=deriv1(x+dx/2,y+k2/2)*dx
k4=deriv1(x+dx ,y+k3 )*dx
RETURN k1/6 + k2/3 + k3/3 + k4/6
Listing 3 shows the core operations performed by the Entity RK4 each time it enters the Location integrators. At the end of the operations block, RK4 is ROUTEd either back to the beginning (using the CONTINUE rule) or, if an interrupt has started the integration of a new segment, to the EXIT. The listed procedure performs a 4th order Runge-Kutta integration with adaptive time stepping, speculative computation, and threshold detection. When the threshold condition is met, the type 3 interaction is effected by issuing a SEND statement to the Entity waiting at the furnace Location.
Numerical integration processes, turned off when not needed, can be spawned by ORDERing a dummy entity to a real or dummy location. Listing 4 shows the operations typical for such an Entity, here Intr2 at integrators. It performs the initialization appropriate to its type and then spawns the recurring process by routing another Entity RK4 back to the same Location.
Listing 3: Asynchronous Numerical Integration Operations
###############################################################
# OPERATIONS BLOCK FOR ENTITY RK4 AT LOCATION integrators #
# This block implements a simple fourth order Runge-Kutta
# integration with adaptive time step control. #
# refer to Press, et al. Numerical Recipes in C, 2nd Ed. #
# pp. 710-716 #
###############################################################
# DECLARE LOCAL VARIABLES
#--------------------------------------------------------------
¶INT retry # flag controlling adaptive stepper
INT too_slow, too_sloppy # flags reflecting truncation error
REAL max_err=max_error_per_RK_step, min_err=max_err/100.0
REAL y_1step,y_2step,t_err # interim results
# SAVE THE CONTEXT IN
ATTRIBUTES
#--------------------------------------------------------------
LocAttr1=CLOCK() # use these later for intr handling
EntAttr1=CLOCK()
# COMPUTE SPECULATIVE
TEMPERATURE AND TRUNCATION ERROR
#--------------------------------------------------------------
DO BEGIN # until retry=False
y_1step=Temp+dy_rk4(CLOCK(HR),Temp,time_step)
y_2step=Temp+dy_rk4(CLOCK(HR),Temp,time_step/2)
y_2step=y_2step+dy_rk4(CLOCK(HR)+time_step/2,y_2step,
time_step/2)
t_err=y_2step-y_1step # Press 2nd. p.715 16.2.2
# DECIDE WHETHER RESULT IS
WITHIN ACCURACY SPECIFICATIONS
#------------------------------------------------------------
IF abs(t_err)<min_err THEN too_slow=True
ELSE too_slow=False
IF abs(t_err)>max_err THEN too_sloppy=True
ELSE too_sloppy=False
retry=TRUE
IF too_slow=True THEN time_step=2*time_step # double
ELSE IF too_sloppy=True THEN time_step=time_step/2 # half
ELSE retry=False # just right
END UNTIL retry=False
# This completes the
computation of the speculative result
# for the temperature at time_step in the future.
# Keep the best value in the (local) variable, y_2step:
y_2step=y_2step+(t_err/15.0) # Press 2nd. p. 715 16.2.3
# CHECK FOR THRESHOLD
CROSSING (Type 3 Interaction)
#--------------------------------------------------------------
IF y_2step>=Tthreshold THEN BEGIN
# interpolate time to crossing
time_step=time_step*(Tthreshold-Temp)/(y_2step-Temp)
WAIT time_step
Temp=Tthreshold
SEND 1 Workpiece TO cooling
# Output Destination Rule
ROUTE 2 BREAK END # RK4 EXIT FIRST 1
# WAIT FOR SIMULATION CLOCK
TO CATCH UP
#--------------------------------------------------------------
WAIT time_step
# DECIDE WHETHER THERE HAS
BEEN AN INTERRUPT
#--------------------------------------------------------------
IF LocAttr1=EntAttr1 # no interruption
THEN BEGIN
# Publish the speculative result as the global variable Temp
Temp=y_2step
# Then go back for another bite
# Output Destination Rule
ROUTE 1 END # RK4 integrators CONTINUE 1
ELSE BEGIN # interruption
# Output Destination Rule
ROUTE 2 BREAK END # RK4 EXIT FIRST 1
Listing 4: Type 2 Interaction Operations
# Intr2 Type 2 Interaction
Preamble
#--------------------------------------------------------------
# update the value of the continuous variable first
REAL short_step
# calculate the size of the short step
short_step=CLOCK()-LocAttr1
# call the integration routine for a new Temp.
Temp=Temp+dy_rk4(CLOCK(),Temp,short_step)
# restart the integration
time_step=0.05
# exit ROUTING: Output Destination Rule
# RK4 integrators FIRST 1
Extend from Imagine That! is a visual simulation modeling language that has support libraries for either discrete or continuous systems. Combined models are constructed in the discrete mode. While Extend has library support for integration of continuous variables in discrete models, that support is based on a fixed time step size Euler method. In the context of issues discussed in this paper, that support lacks the speed, accuracy and stability that are required for high performance modeling.
However, Extend, as part of its C legacy,
inherits a rich and expressive underlying structure along with
its built-in ModL language. ModL has an expressive data structure
that includes user-definable real, integer, string, and array
types (though no structures). In addition, Extend's block
structure supports message passing among processes and
programming of the block responses to those messages. Figure 7
shows one approach to modeling a combined process in Extend. The
required behavior of the furnace block (receiving an item,
triggering the integration process, and passing the item on after
receiving a release message from the integrator) may be obtained
by modifying one of Extend's existing library blocks. The
user-written integration block may be triggered either by a
message to Intr2In or, if the model required that item attributes
be passed to the integrator, the item itself could be passed. The
numerical integration itself is coded into the integrator block
script. When the threshold temperature was reached, then the
integrator block sends a message to the furnace via the Intr3Out
connection.
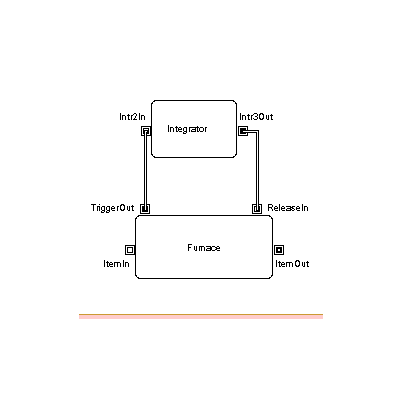
Figure 7: Block Interactions in Extend (TOC)
Of the examined modelers none explicitly supports combined models with the features required for high performance. ProModel for Windows has no built-in support at all. Extend supports either discrete event or continuous models, but its support for continuous variables in combined models is suitable only for small or undemanding problems.
Although ProModel for Windows and Extend have
different modeling paradigms, both have data structures and
programming features that enable construction of robust combined
models. The methods described implement speculative computation,
a robust integration scheme, adaptive time step adjustment,
threshold detection, and asynchronous restarts after
interruption. The ability to use different time step sizes for
processes that have different time characteristic and the ability
to turn off numerical integration when it is not needed are
crucial advantages of the approach. (TOC)
FREDERICK KLINGENER is president of Brock Engineering, P. C. in Roxbury Connecticut. He received a B. S. in 1962 and an M.S. in 1966 in mechanical engineering from Carnegie Institute of Technology. He is a registered mechanical engineer in the state of Alaska. He has had broad experience in design, analysis, and fab-rication of nuclear, robotic, and automotive mechanical systems. He has recently worked in cost, risk, and production analysis of the army's program to dispose of unserviceable chemical weapons. Mr. Klingener's current interests include data analysis of real and simulated manufacturing processes. (TOC)
Return to the top of
the Brock Engineering home
page.
Your comments and suggestions are welcomed at klingener@BrockEng.com
or at (860) 354-7069
Revised: 03/11/98 6:09 PM
| REVISION HISTORY | ||||||
| content | 07-15-96 | submit camera-ready draft | ||||
| html | 07-17-96 | format for html | ||||
| 09/12/96 04:30 PM | add TOC, bookmarks, renumber 4.3, 4.4; change to l.c. | |||||
| 09/13/96 12:42 PM | adjust headers, footers | |||||
| 12/15/96 12:48 PM | add WSC 1996 copyright | |||||